1. Wstęp
Czy wiedzieliście, że pierwszych pomiarów odległości do ciał niebieskich próbowano już w starożytności? Za pomocą zwykłego kijka, prawie 2300 lat temu zmierzono obwód i średnicę Ziemi. Dzięki zaćmieniu Księżyca i Słońca oraz monety obliczono średnicę i odległość do Księżyca. Za pomocą połówki Księżyca i podstaw geometrii wyliczono odległość do Słońca i jego średnicę! Jak tego dokonano?
2. Obwód i średnica Ziemi - Eratostenes - 235 r. p.n.e.
Jak obliczono obwód i średnicę Ziemi? To dzieło Eratostenesa - greckiego matematyka, filozofa i poety. W 255 r. p.n.e. przeniósł się do Aleksandrii, do Egiptu. W 235 r. p.n.e. podczas przeglądania Biblioteki Aleksandryjskiej, natrafił on na bardzo ciekawy zapis:
W mieście Syene (obecnie Asuan), w Egipcie - co roku, w dzień przesilenia letniego (21 czerwca), w momencie górowania Słońca zachodzi ciekawe zjawisko. Wszystkie stojące kolumny wykazują pewną cechę - nie rzucają cienia.
Eratostenes, będąc w Aleksandrii (ok. 800 km na północ) zastanawiał się jak to możliwe i był bardzo tym zaciekawiony, więc postanowił sprawdzić czy w Aleksandrii również takie zjawisko zajdzie. Więc w dzień przesilenia letniego, w czasie górowania Słońca wbił pionowo palik w ziemię i było całkiem inaczej, gdyż palik rzucał cień.
 |
| Eratostenes |
Obwód Ziemi
Eratostenes doszedł do wniosku, że jeżeli światło Słońca pada równolegle na powierzchnię i w różnych miejscach cień jest rzucany inaczej - to oznacza to, że powierzchnia Ziemi jest zakrzywiona i musi być kulista.
Eratostenes wpadł na genialny pomysł jak obliczyć obwód Ziemi. Wystarczyło znać odległość ze Syene do Aleksandrii. Od przewodników karawan Eratostenes wiedział, że odległość pomiędzy tymi miastami wynosi ok. 5000 stadionów. W przeliczeniu wychodzi ok. 800 km.
Eratostenes wyliczył kąt padania cienia i wyszła mu wartość ok. 7,2 stopnia. 7,2 stopnia to mniej więcej 1/50 pełnego okręgu (7.2 x 50 = 360 stopni). Wystarczy tą odległość (ze Syene do Aleksandrii) pomnożyć 50 razy, by uzyskać obwód Ziemi (pełny kąt 360 stopni).
800 km x 50 = 40 000 km
Grecki uczony pomylił się zaledwie o parę procent (w przeliczeniu na km podał wartość w granicach od 39 690 km do 46 620 km). Obecnie wiemy, że obwód Ziemi wynosi ok. 40 075 km. Do dziś używa się tej metody do dokładnego wyznaczenia obwodu i średnicy Ziemi.
Średnica Ziemi
Znając obwód Ziemi można obliczyć promień i średnicę naszej planety. A jak to zrobić? Wystarczy podstawić wartości do wzoru na obwód koła! Wzór na obwód koła:
2π * r
r - promień
π (liczba pi)= 3.1415926
Podstawiamy do wzoru:
2π * r = 40 075 / : 2
π * r = 20037,5
3.1415926r = 20037,5 / : 3,1415926
r = 6378,13
Wyszło nam, że promień Ziemi wynosi ok. 6378 km. Średnica Ziemi to dwukrotność promienia - więc średnica Ziemi wyjdzie nam ok. 12756 km.
Średnica Ziemi wg Wikipedii wynosi 12 742 km, a promień 6371 km. Takie przekłamania powoduje liczba pi. Im więcej miejsc po przecinku, tym dokładniejszy wynik.
3. Średnica Księżyca - Arystarch z Samos - zaćmienie Księżyca.
Znając średnicę Ziemi - możemy też obliczyć średnicę Księżyca! A jak to zrobić? Takiego pomiaru dokonał grecki astronom - Arystarch z Samos.
Do pomiaru średnicy Księżyca wykorzystał zjawisko zaćmienia Księżyca. Podczas zaćmienia Księżyca - cień Ziemi przechadza się przez tarczę srebrnego globu. Miał on okazję takie zaćmienie zaobserwować.
 |
| Kolaż złożony z kilku zdjęć wykonanych podczas zaćmienia Księżyca. Autor: Tragoolchitr Jittasaiyapan / Shutterstock. |
Dzięki obserwacjom oszacował, że cień rzucany na srebrny glob jest 2,5x większy od niego. Oznaczałoby to, że Księżyc jest ok. 2,5 raza mniejszy od Ziemi.
ALE!
Cień Ziemi ulega również zwężeniu (gdyż Słońce jest większe od Księżyca). Trzeba tylko wyliczyć ten stopień zwężenia cienia. Kiedy to zrobić? Najlepiej podczas odwrotnej sytuacji - przy zaćmieniu Słońca. Wtedy to Księżyc rzuca swój cień na Ziemię. Trzeba znać mniej więcej jak duży jest obszar, gdzie Słońce jest przykryte w całości.
Na tej podstawie ostatecznie Arystarch oszacował, że:
Średnica Księżyca - jest ok. 3,5 raza mniejsza od średnicy Ziemi.
12 742 : 3,5 = ok. 3640,5 km
Wg. Wikipedii średnica Księżyca wynosi ok. 3474 km. Średnica Księżyca jest ok. 3,66 raza mniejsza.
 |
| Porównanie rozmiarów Ziemi i Księżyca. |
4. Odległość do Księżyca - moneta
Jak obliczyć odległość do Księżyca znając jego średnicę? Tego również dokonał Arystarch. Wystarczy znać rozmiar kątowy Księżyca. Jeżeli nie znamy jej dokładnie - jest inny sposób:
Weźmy sobie monetę. Ustawmy ją sobie w takiej odległości od oka, by ta moneta przykryła w całości tarczę Księżyca. Kąt zawarty między długością ramienia a okiem nie zmienia się aż do samego Księżyca, więc teraz musimy obliczyć stosunek odległości do tej monety oraz jej średnicy.
Arystarch oszacował, że średnica monety jest 110x mniejsza niż odległość od oka do monety. A to, że kąt zawarty między okiem a monetą nie zmienia się aż do Księżyca - oznacza to że:
Odległość do Księżyca - jest również 110 razy większa niż średnica Księżyca.
3474 x 110 = ok. 382 140 km
Więc można oszacować że odległość Ziemi do Księżyca to mniej więcej 382 140 km.
5. Odległość do Słońca - Arystarch z Samos
A co ze Słońcem? Zmierzenie odległości do Słońca nie jest już takie proste jakby się mogło wydawać. To kolejne dzieło Arystarcha z Samos. Ta metoda pokazuje ogromny geniusz tego człowieka!
Do wyznaczenia odległości do Słońca Arystarch wykorzystał: Słońce, Księżyc (w fazie pierwszej lub ostatniej kwadry) oraz Ziemię, tworząc z nich gigantyczny trójkąt prostokątny.
Czasami jest taka sytuacja, że na niebie widać jednocześnie Słońce i Księżyc, a Księżyc oświetlony jest w połowie. Wtedy Ziemia, Słońce i Księżyc tworzą trójkąt prostokątny.
Suma wszystkich kątów w każdym trójkącie wynosi 180 stopni. Gdybyśmy znali wszystkie kąty oraz co najmniej jeden bok - można obliczyć długości innych boków - jak np. odległość do Słońca.
Jeden z kątów jest prosty i wynosi 90 stopni. Potrzebujemy jeszcze jednego kąta by obliczyć trzeci kąt.
Jak obliczyć taki kąt?
Wystarczy obliczyć podczas pierwszej lub ostatniej kwadry (idealnej połówki Księżyca) kąt zawarty między Księżycem, a Słońcem.
Współczesne pomiary dają wartość 89 stopni i 51 minut (wymaga to precyzji niemożliwej do osiągnięcia w starożytności). Arystarch swoimi prostymi metodami wyliczył ten kąt na wartość 87 stopni.
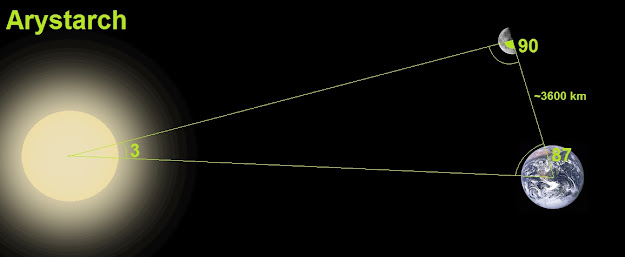 |
| Skala nie jest zachowana. |
 |
| Skala nie jest zachowana. |
Potrzebujemy jeszcze tylko długości jednego boku - a mamy go - jest to oczywiście odległość Ziemi do Księżyca. Arystarch dzięki swoim obliczeniom obliczył odległość Ziemi do Słońca na 19 krotność odległości Ziemi do Księżyca.
Niestety!
Niestety, jego obliczenia były bardzo niedokładne. W rzeczywistości Słońce nie jest 19 razy dalej niż Księżyc, a 400 razy dalej! Takie przekłamanie spowodowało, że drugi kąt zawarty między Słońcem i Księżycem jest prawie prosty i nawet najmniejsza zmiana powoduje ogromne przekłamania!
Wynik może nie był zbyt precyzyjny, ale sam pomysł - był wręcz genialny!!!
Średnica Słońca
Pamiętacie doświadczenie z Księżycem i monetą powyżej? To samo można zrobić ze Słońcem. Dzięki temu, że Słońce i Księżyc mają prawie że identyczny rozmiar kątowy - to można stwierdzić tak samo - że odległość do Słońca jest 110x większa niż średnica Słońca.
A czy to prawda? Sprawdźmy to:
Odległość Ziemi do Słońca (średnia): 149 600 000 km
149 600 000 : 110 = 1 360 000 km
Średnica Słońca (wikipedia) = 1 392 000 km
Czyli się mniej więcej zgadza. Trzeba też wziąć pod uwagę, że Odległość do Słońca czy Księżyca nie są stałe (Ziemia i Księżyc mają eliptyczne orbity).
Jeżeli wam się podobało to udostępnijcie i napiszcie w komentarzu jakieś propozycje o czym napisać. Pozdrawiam, McGoris :)
Zapraszam także do polubienia strony na Facebooku: facebook.com/mcastronomia
ZOBACZ TEŻ:



Świetny i zwięzły artykuł! W bardzo przystępny sposób opisałeś, jak to zostało zrobione. Dzięki za kawałek wiedzy :) Pozdrawiam, Maćko
OdpowiedzUsuńDziękuję za artykuł. Bardzo pomocny i zwięzły.
OdpowiedzUsuńMyślałem, że przed Kopernikiem zawsze myślano, że ziemia jest płaska, a jednak nie.. Bardzo ciekawy artykuł, dzięki!
OdpowiedzUsuńŚwietny materiał
OdpowiedzUsuń